Computational Design of Polyomino Puzzles

Naoki Kita†
Kazunori Miyata‡

CGI 2020

teaser image

Abstract

People of all ages enjoy solving geometric puzzles. However, finding suitable puzzles, e.g., puzzles with a moderate level of difficulty or puzzles with intellectually stimulating shapes can be difficult. In addition, designing innovative and appealing puzzles requires demanding effort and, typically, involves many trial and error processes. In this paper, we introduce a computational approach for designing geometric puzzles. Existing approaches employ bottom-up, constructive algorithms to generate puzzle pieces; therefore, intervening in the piece generation procedure is difficult. Differing from existing approaches that generate puzzles automatically or semi-automatically, we propose a top-down, partitioning-based approach, that enables us to control and edit piece shapes. With a subtle modification, the proposed algorithm can be easily extended to both 3D polycube and 2D polyomino puzzle design. To generate a variety of piece shapes, the proposed approach involves a capacity-constrained graph partitioning algorithm combined with polyomino tiling. We demonstrate the versatility of the proposed approach through various example designs, including fabricated puzzles, created using the proposed method.

Results

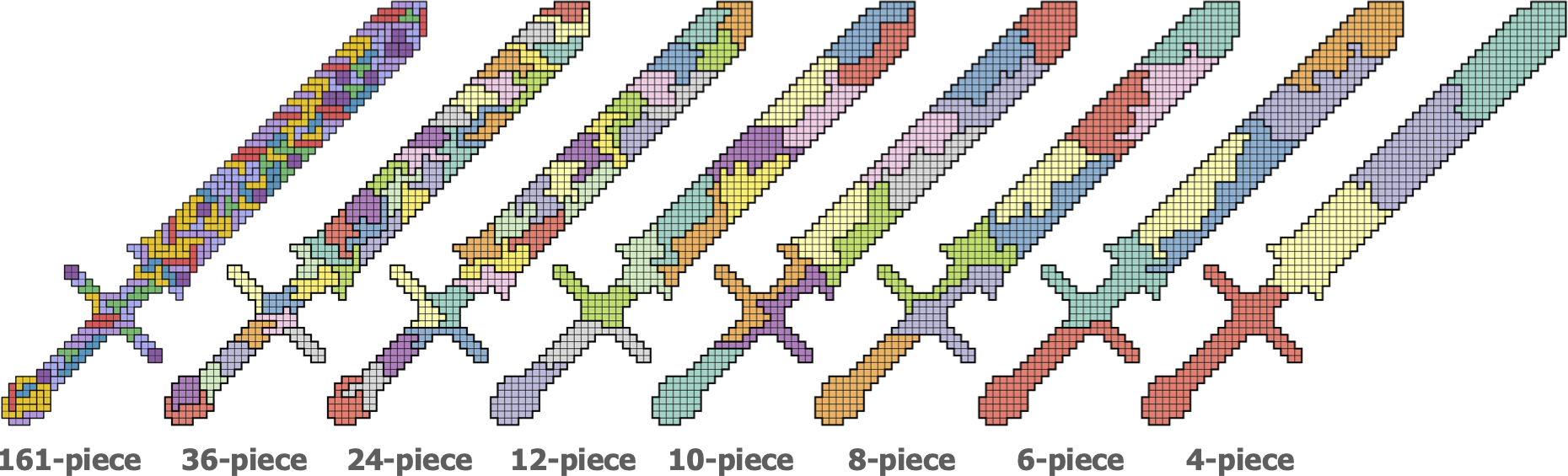
Sword results
Heart results
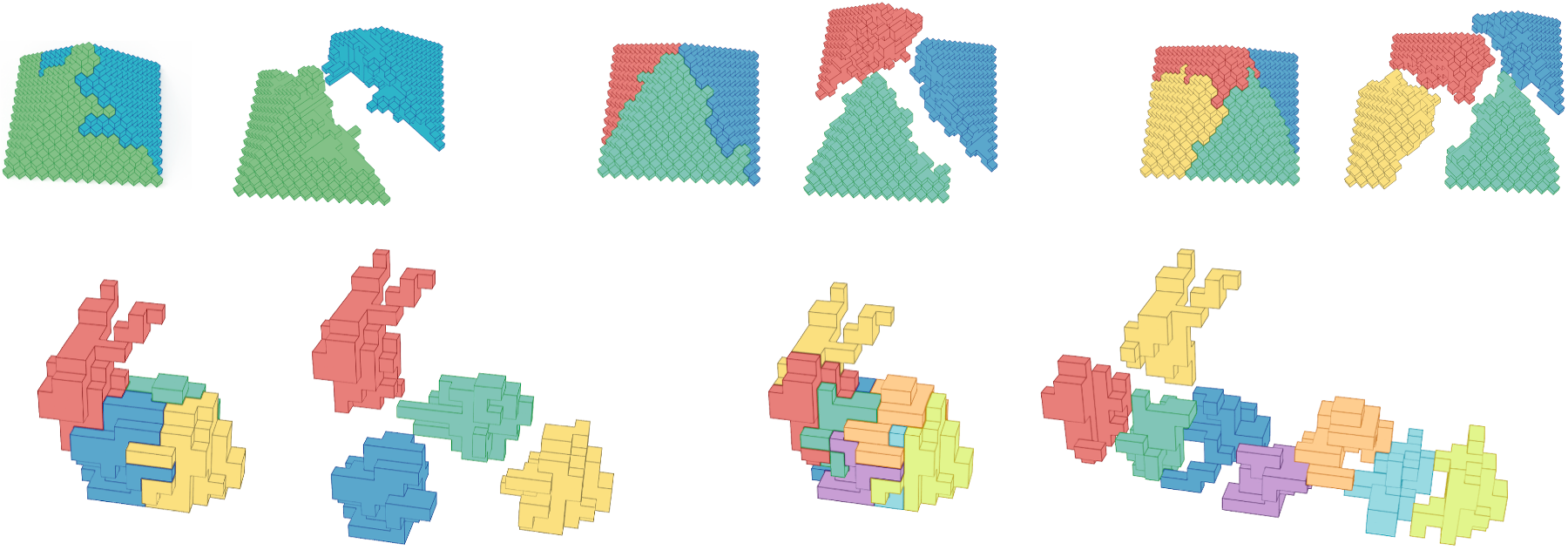
3D results

Links

Acknowledgements

This work was supported by JSPS KAKENHI Grant numbers 19K24338 and 20K19944.

Bibtex

@article{Kita:CGI2020,
  title = {Computational design of polyomino puzzles},
  author = {Kita, Naoki and Miyata, Kazunori},
  year = {2021},
  journal = {The Visual Computer},
  volume = {37},
  number = {4},
  issn = {1432-2315},
  pages = {777--787},
  url = {https://doi.org/10.1007/s00371-020-01968-5},
  doi = {10.1007/s00371-020-01968-5},
}